Lo spazio e i sistemi di riferimento

Lo spazio, come il tempo è alquanto difficile da definire..
Lo spazio considerato in Meccanica come un “luogo” in cui avvengono i fenomeni fisici ed è quindi percepito quotidianamente attraverso l’esperienza.
Esso possiede delle proprietà:
Omogeneità: si dice omogeneo uno spazio dove non ci sono punti privilegiati rispetto ad altri.
Isotropia: si dice isotropo uno spazio dove non ci sono direzioni preferite ad altre.
Lo spazio in Meccanica è quindi omogeneo e isotropo ed è descrivibile attraverso la geometria euclidea.
Sistema di riferimento
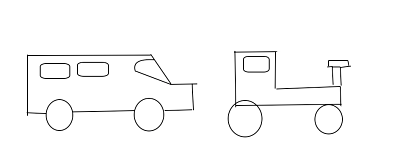
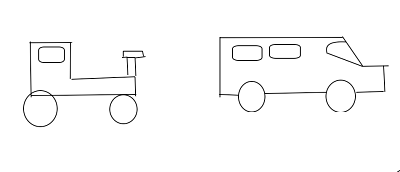
Osservando le due immagini non siamo in grado di dire in modo più che sicuro se è il trattore ad essersi spostato, se è l’autoveicolo ad essersi spostato oppure se si sono spostati entrambi.
Questo dubbio è dovuto alla mancanza di un riferimento visivo. Uno stesso oggetto può infatti essere fermo e in quiete rispetto a determinati soggetti. Se prendiamo ad esempio un individuo su un bus, egli è fermo sul bus, ma il bus verrà percepito in movimento da un altro individuo che aspetta alla fermata.
Siamo quindi in grado di distinguere il movimento di un corpo solo se ne osserviamo i cambiamenti di posizione rispetto ad altri corpi, che fungono da elementi di riferimento. Il moto deve poi essere considerato qualcosa di relativo.
L’insieme dei corpi o degli oggetti rispetto ai quali descriviamo il moto è chiamato sistema di riferimento. Esso è quindi l’insieme dei riferimenti utili ad individuare la posizione di un corpo nello spazio considerato.
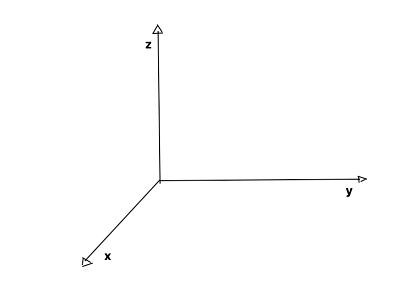
In fisica il sistema classico di riferimento è costituito da tre rette (o assi) perpendicolari tra di loro in modo reciproco.
La posizione (all’istante t) di un punto materiale è il numero reale che definisce la distanza dall’origine di quest’ultimo lungo l’asse cartesiano che viene preso in considerazione in quella situazione. Questo valore è chiamato anche coordinata cartesiana.
La traiettoria di un corpo è invece l’insieme dei punti di posizione occupati successivamente. Da qui vale la pena introdurre il concetto di moto rettilineo.
Il moto rettilineo è definito in base alla sua traiettoria, ovvero una linea retta.
Mentre per descrivere lo spostamento del corpo da un istante x(ti) a un altro istante x(tf) si userà la grandezza spostamento , chiamata anche variazione di percorso e descritta dalla seguente relazione matematica:
Δx (ti,tf)= x(tf) – x(ti) o meglio Δx= xf – xi
Home
Contatti

In uno spazio-tempo deformato, un sistema di riferimento inerziale e definibile solo localmente, a causa della deformazione dello spazio-tempo causata dalla materia.