Grandezze scalari e grandezze vettoriali
Sono dette grandezze scalari quelle che sono pienamente definite attraverso un valore numerico espresso grazie alla sua unità di misura.
Le grandezze vettoriali necessitano , oltre che a informazioni di intensità anche di specificazioni riguardo all’orientamento nello spazio.
Un’esempio di grandezza vettoriale è il vettore geometrico, cioè una qualsiasi grandezza rappresentabile con un segmento di retta orientato e definito da:
- Un modulo, definito da un numero ( sempre positivo) che corrisponde alla lunghezza del segmento.
- La direzione, che indica la retta su cui giace il segmento o una ad essa parallela.
- Il verso, che da l’orientazione del segmento
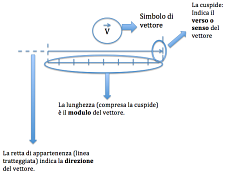
Proprietà dei vettori geometrici:
Se le rette alle quali appartengono due vettori sono parallele i due vettori si dicono paralleli o collineari.
Due vettori paralleli si dicono concordi se hanno lo stesso verso, se hanno verso opposto si dicono opposti o discordi.
Due vettori si dicono equipollenti se se sono paralleli, si equiversi e se hanno la stessa lunghezza
Si dice vettore applicato un vettore al quale è associato un dato punto iniziale, detto punto di applicazione.
